Changepoint algorithm for MCMC

Introduction

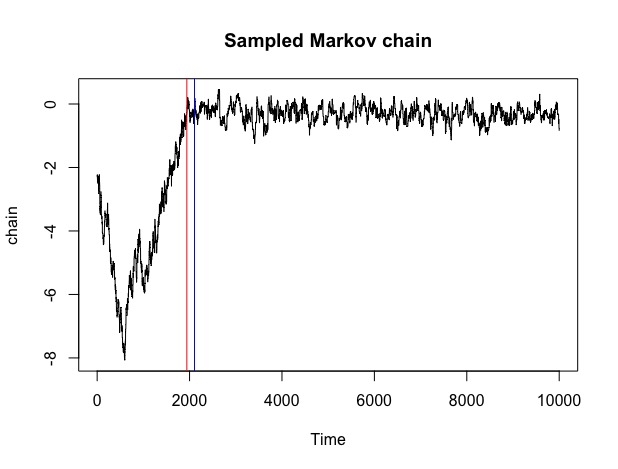
We propose a novel change-point algorithm for the MCMC setup. In particular, we show how procedures based on the cumulative sum, CUSUM, statistics can be modified to work for data exhibiting serial dependence such as a Markov Chain. This allows us to find mean structural breaks under a non-parametric framework, without any strong assumptions on the underlying distribution. We argue that this helps us identify the ideal “burn-in” period for the chain, and subsequently improves the MCMC estimates.

Literature Review

The existing literature on a non-parametric change point analysis is wide, however, a discussion on using change-point methods to identify the initial “transient” (or “burn-in”) period seems to be missing. In particular, the methods based on the CUSUM max-type statistics described in Aue and Horv́ath (2013) suffer from a few major shortcomings as described below.

• The CUSUM method described is “offline” in the sense that while we’re dealing with sequential data, the chain is not processed in a strictly sequential (or “online”) sense. Max-type statistics that operate on the whole chain generally identify the most significant change-point rather than the first significant one. Hence, we require methods that are tuned to identify change-point in the initial part of the chain.

• The power of a max-type statistic is maximum when the two fragments of data are of roughly equal size and is significantly affected when we move to either side.

• Another cause for concern in hypothesis based testing is the assumption of stationarity as the null hypothesis. These methods require the estimation the long-run variance-covariance matrix under the stationarity assumption. However, the chain is often not stationary; the estimates are biased and tend to affect the performance of the test.

• Another potential source of error are multivariate chains with high correlation among components. Normalising CUSUM by the covariance estimator tends to bias the change-point towards the faster converging components.

To summarize, a method that is robust to changes after the first significant change-point, avoids hypothesis based testing and variance estimation is of interest.

For more information, check out the code and pdf, accessible via the buttons on the top.